
Adding floating-point maths capability to microcontrollers expands the design space in multiple directions. The performance of a floating-point unit (FPU) can be exploited to increase the range and precision of mathematical calculations; or it can enable greater throughput in less time, making it easier to meet real-time requirements; or, by enabling systems to complete routines in less time and to spend more time in sleep-mode, it can save power and extend battery life.
by Haakon Skar, AVR Marketing Director, Atmel
Floating point numbers
Floating point numbers – in the form A x 10B – are so-called because in that number representation, the decimal point in the first part of the number (A, the “mantissa” or “significand”) is free to float; you can place it anywhere, according to what best suits whatever calculation you happen to be carrying out, and adjust the value of the exponent (B) to keep the magnitude of the overall number unchanged. See Figure 1 1.234 x 106 is identical with 1234 ? 103. The most common practice is to present – and store – numbers in a normalised form with the point placed after the first non-zero digit.
To the engineer working with digital representations of real-world signals – such as high-quality audio – a large part of the value of using floating point mathematics for processing lies not in the freedom to place the decimal point anywhere, but in the range of numbers that the notation can represent. The most frequently employed standard within computing

and signal processing is IEEE 754, and in that scheme a so-called single-precision number can have a value within a (decimal) range of approximately –1039 to +1039. The floating point notation is a complete subject in itself, and an internet search on the topic, or on IEEE 754, will yield far more detail than most non-mathematicians will wish to tackle, including how the binary storage of numbers is handled, how “special” numbers – such as zero – are accommodated, and the detail distinctions between floating-point, fixed-point and integer arithmetic.
No matter where the number lies in the overall range, the mantissa part always has some 23 bits of resolution, making it a good match for signal content such as 24-bit audio.
Maintaining signal fidelity
The fundamental challenges faced by the engineer designing an audio signal chain have not changed since the context moved from analogue to digital domains. Audio signals have large dynamic ranges with information, critical to faithful reproduction of the content, which must remain uncompromised at both extremes of the signal range – the loudest and quietest. Throughout an audio signal path, the signal may be filtered, mixed, level shifted, or amplified in multiple processing steps. When the design task was in the analogue domain, the designer had to continually monitor signal levels to keep them above the noise floor, while ensuring that peaks in the content did not get too close to amplifiers’ maximum levels; information was always liable to be lost by adding noise at the low end, or clipping at the peak.
An analogous situation exists when the signal is handled in the digital domain. The data values that represent the content must stay within the overall number range if information is not to be lost, by overflow or truncation. Multiple stages of signal processing, especially filtering, involve successive mathematical operations – especially multiplication – that can shift the absolute value of the data over very wide ranges. With a limited number range, care has to be taken that the “sliding window” of relative values – in the case of audio content, loudest to quietest – stays well within the available range – in the analogue analogy, out of the noise floor but below the voltage rail.
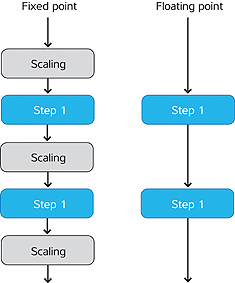
Conventionally, digital signal processing devices that employ floating point arithmetic have been considerably more expensive than their fixed point counterparts. A frequently used methodology has been to develop an initial version of a signal-processing project in the floating-point environment, allowing numerical values to range freely within the vastly greater available numerical space. Then when the algorithms are working according to specification, the prototype is converted to lower-cost fixed-point hardware. Part of that process involves inspecting the numerical values that the, now-working, product generates along the signal chain, and introducing scaling factors at appropriate points to keep the values within the usable number ranges. The reverse approach is also valid; project managers can opt to host designs on more expensive target hardware to shorten, and reduce the costs of the development process.
Process technology enables small FPUs
Both approaches described above are based on the assumption that floating-point co-processors consume substantial amounts of silicon area, leading to expensive devices. However, today’s silicon fabrication technology means that this is no longer necessarily true. It is now possible to pair a 32-bit microprocessor core – of the class that lies at the heart of a mid-range microcontroller – with a fully-IEEE754-compliant floating point unit, in an economically viable unit. For example, Atmel’s AVR UC3 microcontrollers already offer very high digital signal processing performance, with fixed-point and integer arithmetic support; the addition of a single-precision floating point unit changes the options open to designers in a number of ways.
The first, following from the observations above on floating point number systems, is freedom from many detail concerns regarding number ranges and scaling. Through successive processing steps, given the very large range available, the signal value can (to a large extent) be allowed to take whatever absolute value it needs; the essential information – signal dynamic range – will always be contained within the 24-bit fractional number representation of the floating point number mantissa. The need to constantly attend to scaling to keep the number range within bounds disappears.
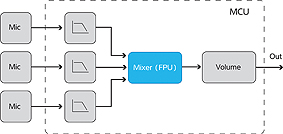
The benefits of an on-chip FPU extend beyond that simple design freedom, however; there is a gain in throughput, as the FPU can perform in a handful of clock cycles, operations such as precision multiply and divide, that consume many tens of cycles in an un-augmented core. In the AVR UC3 devices, the FPU performs most 32-bit floating point instructions in a single cycle, and a 32-bit multiply-accumulate in two clock cycles, compared to the 30-50 cycles required to complete the same arithmetic operation without an FPU. That added throughput could be exploited to greatly increase the amount of signal processing that a microcontroller can accomplish: or, it can represent a significant reduction in power needed to achieve a given output.
MCU + FPU equals a wider application space
There are numerous examples of “mission-critical” system designs, in which code must meet real-time scheduling deadlines, which benefit from the capability to carry out high-precision calculations in few CPU cycles. The automotive power train is a case in point; an engine management unit has to handle sensor inputs with very large dynamic ranges, but the time available to complete each computation cycle is totally defined by the mechanical rotation of the engine. Similar constraints apply to systems such as ABS (anti-lock braking) or active suspension. In precision electric motor control, the ability to handle large number ranges is also valuable because algorithms require that a number of complex transformations are applied sequentially, without loss of data through truncation – however, once again, the time for the computation is set by the rotation period of the motor. In these cases, both precision and speed are valuable benefits. Digital signal processing using FFT (the fast Fourier transform) is an example already familiar to many engineers of problem amenable to acceleration with floating-point maths. In another application space entirely – graphics and publishing systems – the visual quality of results depends on precise geometric calculations that scale graphic textures and printing fonts. Here, there may be lesser real-time limitations but system performance and throughput directly reflect the FPU’s ability to execute calculations in fewer cycles. Each of these sectors has traditionally had access to floating-point, but designers working with microcontroller cores, in general, have not.
The availability of floating point arithmetic in this class of processor alters the dynamics of device selection for many types of design; in particular, consumer audio devices. The audio signal chain dramatically demonstrates the benefit to the designer of employing a floating-point architecture. In many – probably the majority – of cases, the signal source will be a digital representation that can be converted to the required number format in a few cycles. At the end of the signal chain, the audio will be returned to the analogue, real-world domain; after normalisation (a single-cycle operation) a DAC will operate on the fractional-numbers as represented in the mantissa, that carries all the data it needs. Whatever excursions the signal has taken through the full FP number range are simply discarded; the exponent is not used and the maximum precision will have been maintained throughout.
Designers working with signal capture and processing systems in other spheres – industrial systems, or medical instrumentation – who likewise need to perform multiple processing steps on data that itself has a wide dynamic range, will find that the integration of a general-purpose MCU core with an FPU changes their options. Previously, a signal path with processing implemented in floating point inevitably meant a pairing of microprocessor or microcontroller, with a dedicated DSP, with implications in cost, size, and power consumption. The option of placing their complete design on a DSP alone would often be ruled out because the DSP lacked the ability to host the control functions that their project demanded.
Conclusion
The markets usually associated with microcontrollers – where considerations such as ease of interfacing to external signals and events, low cost, and limited power budgets, have tended to prevail – have not previously had access to floating point mathematics.
The very term FPU has carried overtones of complex, high-end, often DSP-based systems. In fact, now that progress in process technology has made the FPU accessible to a much wider range of projects, engineers will gain access to the benefits of computational precision, wide dynamic range and simplified coding that floating-point math brings.
www.atmel.com


